Two Pointers Technique explained with an Example
Two pointers algorithm for sorted arrays explained with an example
Explaination:
Introduction:
Two Pointers technique is an easy and efficient technique used in searching pairs in a Sorted Array.
It works for sorted arrays only so if the array is not sorted, You have to apply any efficient sorting algorithm.
Approaches:
There are two approaches to solving using this technique, right now we are just going through the theory, later it will be more clear to you when we will discuss the illustration.
1. Naive or Brute Force Approach:
Here we maintain two pointers, so for ith pointer, the jth pointer traverses (n-i) positions and check the constraints. If constraints match we return the pairs in whatever form is asked in question else loop gets terminated.
This works for the unsorted array as well!
Code:
for(int i=0; i<sizeOfArray; i++){
for(it j=0; j<sizeOfArray; j++){
// conditions and other code
}
}
Example:
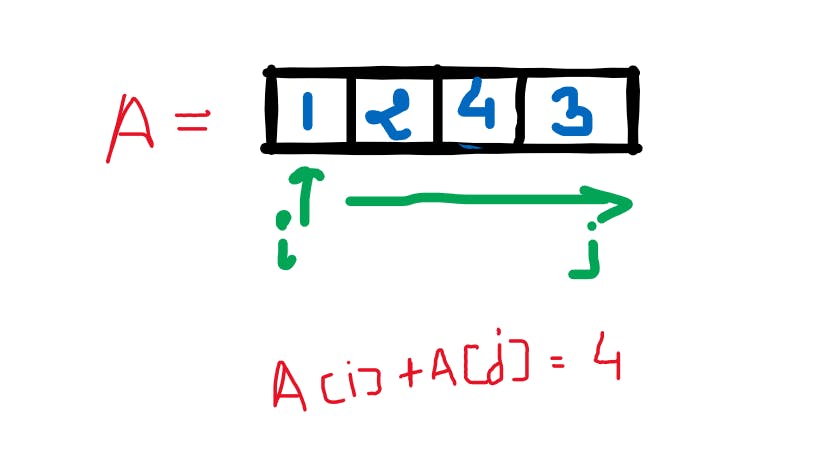
Suppose we have a problem that states:
- Given an unsorted array, return true if the pair of elements within the array whose sum equals 4 else return false.
Idea We use two pointers i and j, For every i, j will run (sizeOfArray - i)th times and check if the sum is 4 or not, If it is, it will return true else it will return false.
Code
// n = size of array
bool isSum(int arr[], int n){
for(int i=0; i<n; i++){
for(int j=0;j<n;j++){
if(arr[i] + arr[j] == 4){
return true;
}else{
return false;
}
}
}
}
Time Complexity:
As you might have already guessed, we are using 2 nested loops, the outer loop runs n times and for every time, the Inner loop runs for (n-1) times. Hence overall in the worst case the time complexity becomes: n(n-1) = n2 - n = O(n2)
2. Efficient Method:
This method works for sorted arrays only!
- In this method we again maintain two pointers but here, we initialize the first pointer at the initial position of the array and the second one to the last position of the array. We then check the condition; according to the given condition, we move the pointers.
- We terminate the movement as soon as both pointers cross each other.
Note: The first pointer cannot move backward and similarly the last pointer cannot move forwards otherwise they will get out of the array boundary.
Code:
// initializing the pointers, n = size of the array
int i=0, j=n-1
while(i<j){
// if condition meets
return
// else move the pointers according to the condition
i++ or j--;
}
Example:
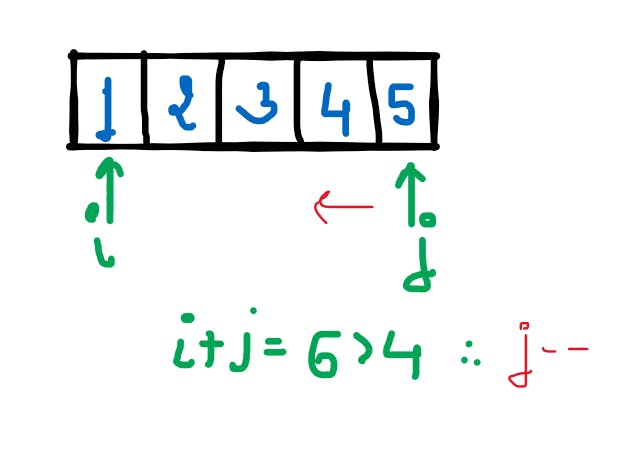
Let's take the above example only for better clarity Suppose we have a problem that states:
- Given an unsorted array, return true if the pair of elements within the array whose sum equals 4 else return false.
Idea We first sort the array if it's not sorted, then we initialize pointers as i=0 and j=sizeOfArray-1 Now we check if the sum of elements at these indices equals 4 or not
- If it's greater than 4, we move j closer to i
- If its smaller than 4, we move i closer to j
The reason for this logic is pretty simple, as the array is sorted, the further we move from the start, the more the sum will become, and similarly the further we move from the end, the more the sum will decrease.
Code
// n = size of array
bool isSum(int arr[], int n){
int i=0, j=n-1;
while(i<j){
if(arr[i] + arr[j] == 4){
return true;
}else if(arr[i] + arr[j] > 4){
j--;
}else{
i++;
}
}
return false;
}
Time Complexity:
Again as you might have guessed, if the array is already sorted, Time Complexity will be O(n) as we are running loop till n in the worst case If the array is not sorted already, we need to sort it and typically the most efficient algorithm takes O(nlogn) time for sorting. Hence, O(nlogn + n) which equals O(nlogn) as n will become less dominating
That's it from my side! I hope you gained some value by reading this, you can practice more on this on platforms like Leetcode, etc.


